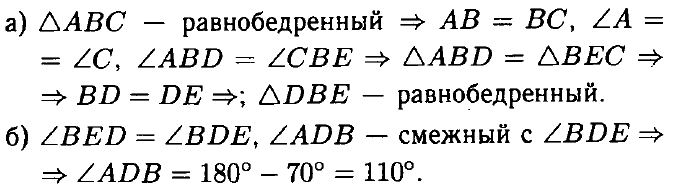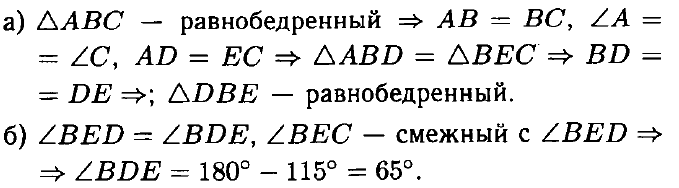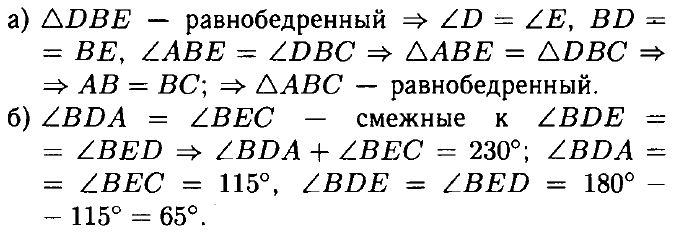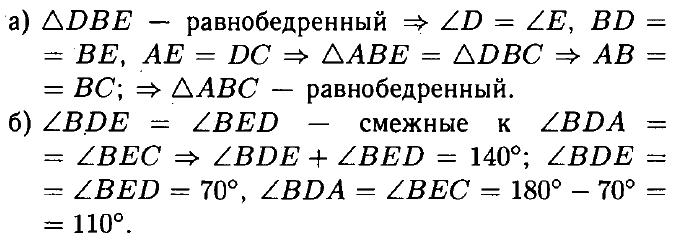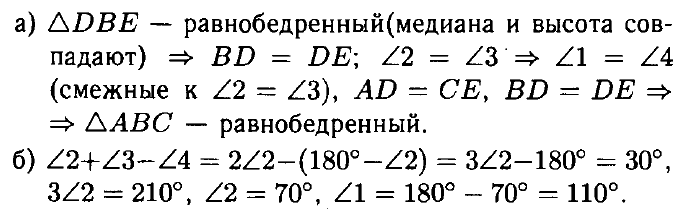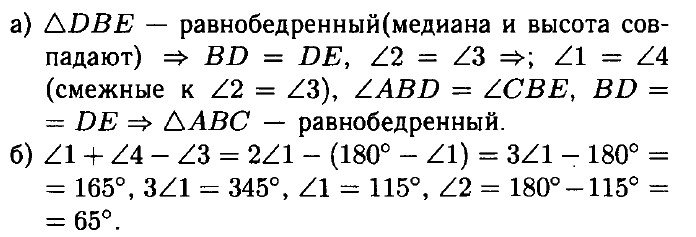Контрольная работа № 2 по геометрии «Треугольники 7 класс» (по учебнику Атанасяна). Пособие адресовано родителям, которые смогут проконтролировать правильность выполнения решения, а в случае необходимости помочь детям в выполнении домашней работы по геометрии. Цитаты из пособия использованы в учебных целях. Ответы на контрольную работу даны в конце статьи.
Контрольная работа рассчитаны на один урок (45 минут) и позволяет осуществить дифференцированный контроль знаний, так как задания распределены по трем уровням сложности А, Б и В. Уровень А соответствует обязательным программным требованиям, Б — среднему уровню сложности, В — для учеников, проявляющих повышенный интерес к математике, а также для использования в классах, школах, гимназиях и лицеях с углубленным изучением математики. Для каждого уровня приведено два расположенных рядом равноценных варианта.
Геометрия (УМК Атанасян)
Треугольники 7 класс
Контрольная № 2 Уровень А (начальный)
ОТВЕТЫ на Вариант А1
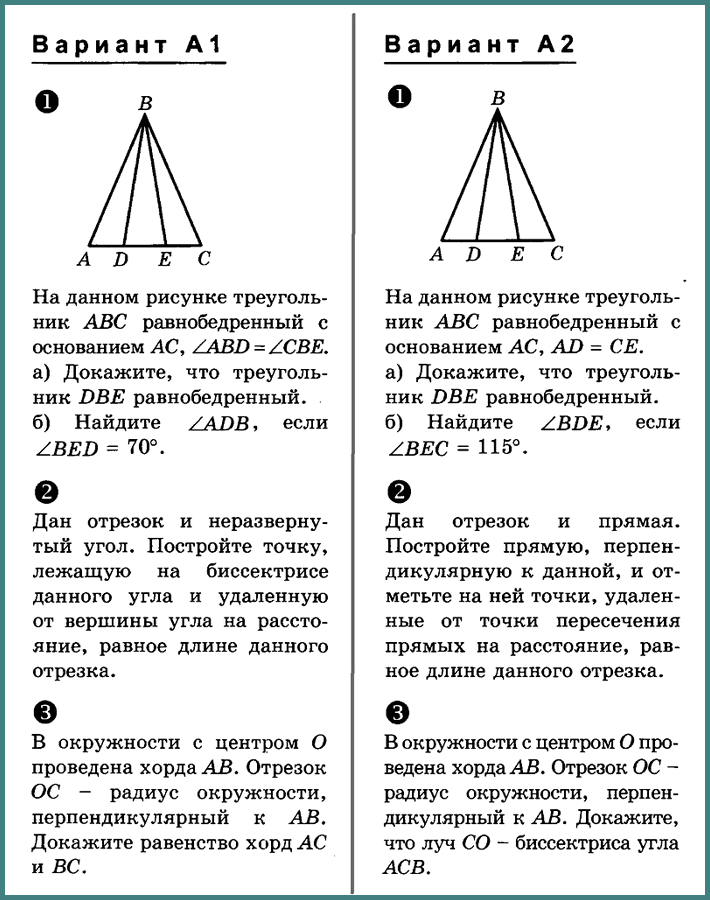
№ 1. На данном рисунке треугольник АВС равнобедренный с основанием АС, ∠ABD = ∠CBE.
а) Докажите, что треугольник DBE равнобедренный.
б) Найдите ∠ADB, если ∠BED = 70°.
ОТВЕТ: б) 110°.
№ 2. Дан отрезок и неразвернутый угол. Постройте точку, лежащую на биссектрисе данного угла и удаленную от вершины угла на расстояние, равное длине данного отрезка.
ОТВЕТ: 1) Из точки В произвольным радиусом проводим дугу MN,
2) Из точки N делаем произвольным радиусом засечку зеленого цвета,
3) Из точки М тем же радиусом делаем засечку красного цвета,
4) Засечки пересекаются в точке L. Соединяем точки В и L – это мы построили биссектрису угла АВС,
5) Циркулем измеряем отрезок а и, не меняя радиуса, из точки на биссектрисе BL делаем коричневую засечку. Она пересечет биссектрису в точке К. Это и есть искомая точка.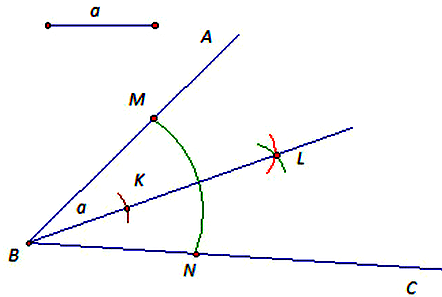
№ 3. В окружности с центром О проведена хорда АВ. Отрезок ОС — радиус окружности, перпендикулярный к АВ. Докажите равенство хорд АС и ВС.
Доказательство 1: По условию, радиус ОС перпендикулярен хорде АВ, то радиус делит хорду пополам. НВ = НА = АВ / 2 (Н – точка пересечения хорды с радиусом). Треугольники АСН и ВСН прямоугольные, у которых катет СН общий, а катет НВ = НА, тогда треугольники АСН и ВСН равны по двум катетам и прямому углу между ними, тогда хорда АС равна ВС, что и требовалось доказать.
Доказательство 2: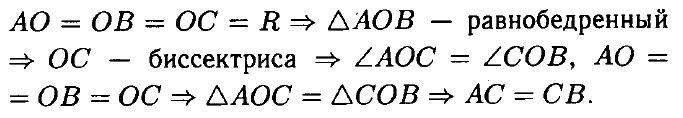
ОТВЕТЫ на Вариант А2
№ 1. На данном рисунке треугольник АВС равнобедренный с основанием АС, AD = СЕ.
а) Докажите, что треугольник DBE равнобедренный.
б) Найдите ∠BDE, если ∠BEC = 115°.
ОТВЕТ: б) 65°.
№ 2. Дан отрезок и прямая. Постройте прямую, перпендикулярную к данной, и отметьте на ней точки, удаленные от точки пересечения прямых на расстояние, равное длине данного отрезка.
ОТВЕТ: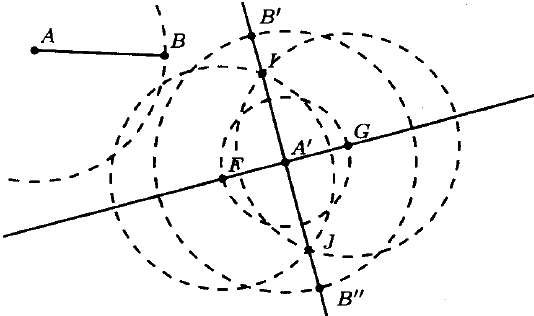
№ 3. В окружности с центром О проведена хорда АВ. Отрезок ОС -радиус окружности, перпендикулярный к АВ. Докажите, что луч СО — биссектриса угла АСВ.
ОТВЕТ: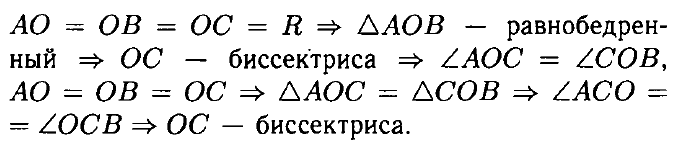
Контрольная № 2 Уровень Б (средний)
ОТВЕТЫ на Вариант Б1
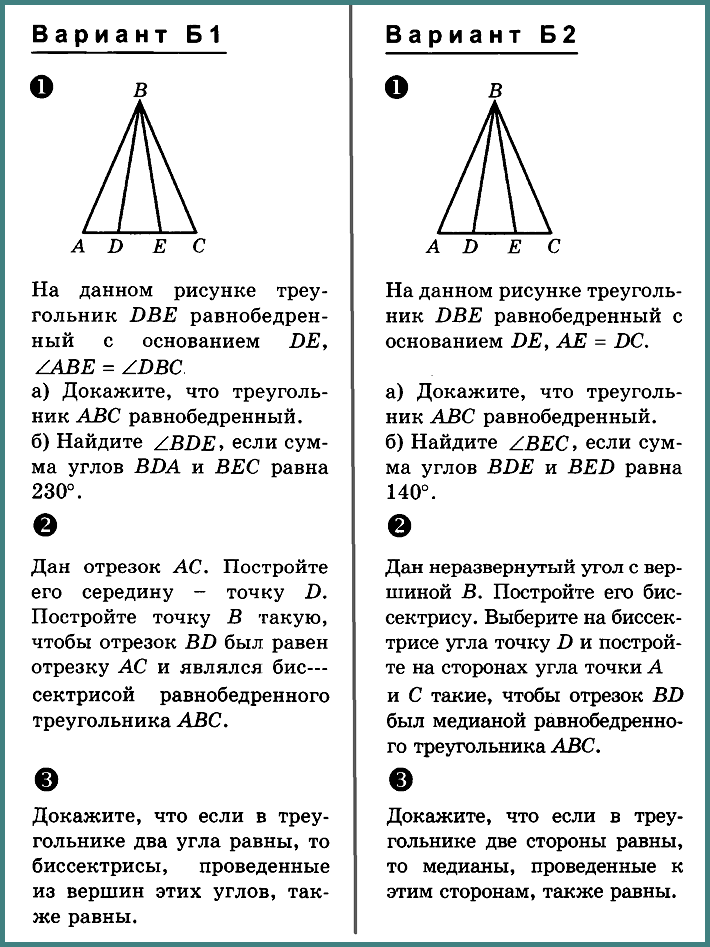
№ 1. На данном рисунке треугольник DBE равнобедренный с основанием DE, ∠ABE = ∠DBC.
а) Докажите, что треугольник АВС равнобедренный.
б) Найдите ∠BDE, если сумма углов BDA и ВЕС равна 230°.
ОТВЕТ: б) 65°.
№ 2. Дан отрезок АС. Постройте его середину — точку D. Постройте точку В такую, чтобы отрезок BD был равен отрезку АС и являлся биссектрисой равнобедренного треугольника АВС.
ОТВЕТ: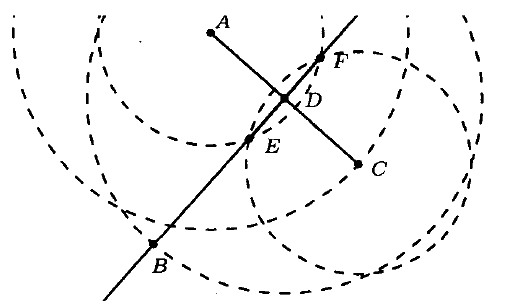
№ 3. Докажите, что если в треугольнике два угла равны, то биссектрисы, проведенные из вершин этих углов, также равны.
ОТВЕТ: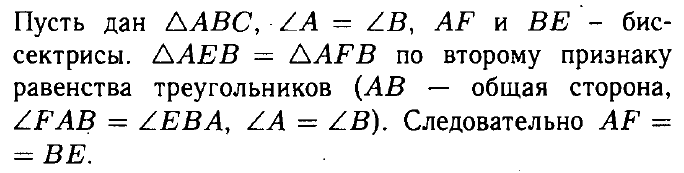
ОТВЕТЫ на Вариант Б2
№ 1. На данном рисунке треугольник DBE равнобедренный с основанием DE, АЕ = DC.
а) Докажите, что треугольник АВС равнобедренный.
б) Найдите ∠BEC, если сумма углов BDE и BED равна 140°.
ОТВЕТ: б) 110°.
№ 2. Дан неразвернутый угол с вершиной В. Постройте его биссектрису. Выберите на биссектрисе утла точку D и постройте на сторонах угла точки А и С такие, чтобы отрезок BD был медианой равнобедренного треугольника АВС.
ОТВЕТ: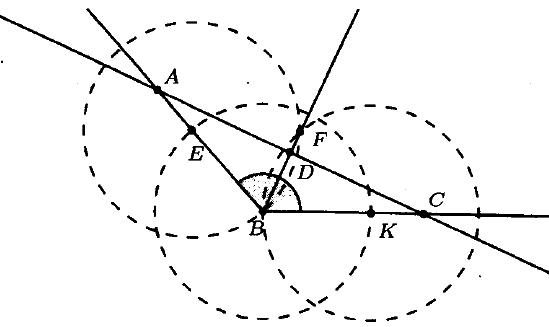
№ 3. Докажите, что если в треугольнике две стороны равны, то медианы, проведенные к этим сторонам, также равны.
ОТВЕТ: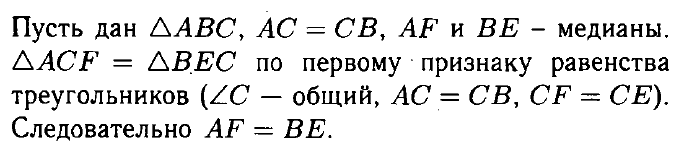
Контрольная № 2 Уровень В (сложный)
ОТВЕТЫ на Вариант В1
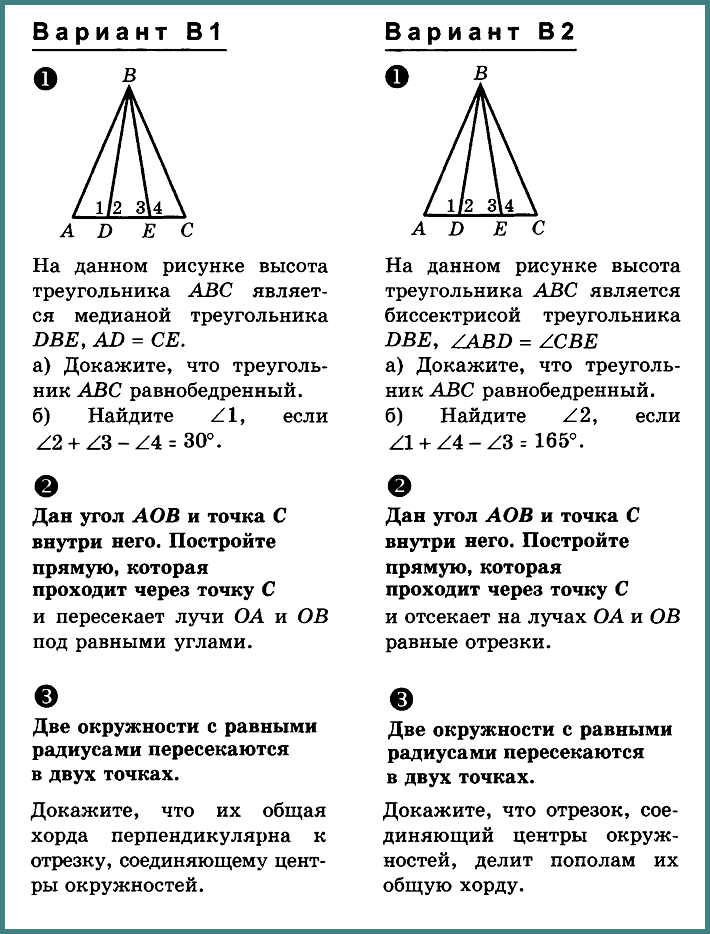
№ 1. На данном рисунке высота треугольника АВС является медианой треугольника DBE, AD = СЕ.
а) Докажите, что треугольник АВС равнобедренный.
б) Найдите ∠1, если ∠2 + ∠3 – ∠4 = 30°.
ОТВЕТ: б) 110°.
№ 2. Дан угол АОВ и точка С внутри него. Постройте прямую, которая проходит через точку С и пересекает лучи ОА и ОВ под равными углами.
ОТВЕТ: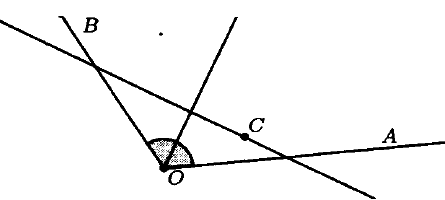
№ 3. Две окружности с равными радиусами пересекаются в двух точках. Докажите, что их общая хорда перпендикулярна к отрезку, соединяющему центры окружностей.
ОТВЕТ:
ОТВЕТЫ на Вариант В2
№ 1. На данном рисунке высота треугольника АВС является биссектрисой треугольника DBE, ∠ABD = ∠CBE.
а) Докажите, что треугольник АВС равнобедренный.
б) Найдите ∠2, если ∠1 + ∠4 – ∠3 = 165°.
ОТВЕТ: б) 65°.
№ 2. Дан угол АОВ и точка С внутри него. Постройте прямую, которая проходит через точку С и отсекает на лучах ОА и ОВ равные отрезки.
ОТВЕТ: Постройте окружность произвольного диаметра с центром в точке О. Соедините отрезком α точки ее пересечения со сторонами угла. Треугольник, который получился, равнобедренный (два радиуса его стороны). Через точку С проведите прямую, параллельную отрезку α. Эта прямая будет отсекать от сторон угла равные отрезки.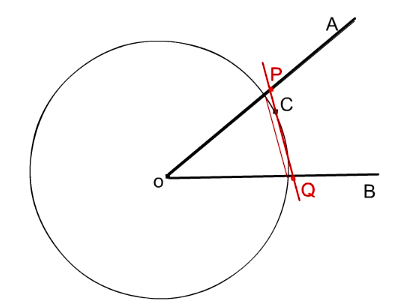
№ 3. Две окружности с равными радиусами пересекаются в двух точках. Докажите, что отрезок, соединяющий центры окружностей, делит пополам их общую хорду.
ОТВЕТ:
Вы смотрели: Контрольная работа по геометрии «Треугольники 7 класс» (по учебнику Атанасяна). Пособие адресовано родителям, которые смогут проконтролировать правильность выполнения решения, а в случае необходимости помочь детям в выполнении домашней работы по геометрии.
(с) Источник: Ершова А.П., Голобородько В.В., Ершова А.С. — Самостоятельные и контрольные работы по алгебре и геометрии для 7 класса. 8-е изд., испр. и доп.— М.: ИЛЕКСА, — 2013. Цитаты из пособия использованы в учебных целях.
Вернуться к Списку контрольных работ